一、算法思想

1. 摩尔投票法

摩尔投票算法（Moore’s Voting Algorithm）是一种用于在数组中寻找多数元素的有效方法。所谓多数元素，是指在数组中出现次数超过一半以上的元素。最经典的例子就是用于众数的寻找。

摩尔投票算法的基本思想很简单，它通过消除不同元素之间的对抗来找到可能的多数元素。算法遍历数组并维护两个变量：候选元素和其对应的票数。开始时，候选元素为空，票数为0。然后对于数组中的每个元素，执行以下步骤：

1. 如果票数为0，将当前元素设为候选元素，并将票数设置为1。
2. 如果当前元素等于候选元素，则票数加1。
3. 如果当前元素不等于候选元素，则票数减1。

这样做的效果是，相同元素的票数会相互抵消，不同元素的对抗也会导致票数减少。由于多数元素的出现次数超过一半以上，所以最终留下的候选元素就很有可能是多数元素。

遍历完整个数组后，候选元素即为多数元素的候选者。然后我们需要进一步验证候选元素是否真的是多数元素，因为可能存在没有多数元素的情况。我们再次遍历数组，统计候选元素的出现次数，如果发现它的出现次数超过了一半以上，则确认它为多数元素；否则，表示没有多数元素。

2. 贪心

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解 。

贪心算法不是对所有问题都能得到体最优解，关键是整贪心策略的选择

贪心算法一般按如下步骤进行：

①建立数学模型来描述问题 。

②把求解的问题分成若干个子问题 。

③对每个子问题求解，得到子问题的局部最优解 。

④把子问题的解局部最优解合成原来解问题的一个解

二、面试150道

2021年的某一天我怀着憧憬进入大学校园，我励志一定要好好学习。那时候室友推荐了力扣这个平台。室友说要成为编程高手必先刷算法题

于是我打开了力扣第一题两数之和…迄今已经过去了四年我再也没有刷过算法题。两数之和也成为一道印象深刻的一道题

有人相爱，有人夜里开车看海，有人leetcode第一题都做不出来。

拖延了四年发现我还是大傻逼

88. 合并两个数组

给你两个按 非递减顺序排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

**注意：**最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

题解

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
       int let1 =m-1;
       int let2=n-1;
       int let=m+n-1;
       while(let1>=0 && let2>=0){
        nums1[let--]= nums2[let2]>nums1[let1] ? nums2[let2--] : nums1[let1--];
       }

        while (let2 >= 0) {
            nums1[let2] = nums2[let2];  
            let2--;
        }
    }
}

思路：

1. 从尾部添加数组元素更加方便一些。
2. 数组1中的末尾元素等于数组2与数组元素1中的较大者
3. 当数组1元素为0时需要将数组2中的所有元素添加到数组1中

27. 移除元素

给你一个数组 nums 和一个值 val，你需要原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

• 更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
• 返回 k。

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2,_,_]
解释：你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3,_,_,_]
解释：你的函数应该返回 k = 5，并且 nums 中的前五个元素为 0,0,1,3,4。
注意这五个元素可以任意顺序返回。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

题解：

class Solution {
    public int removeElement(int[] nums, int val) {
        int let =0;
        for(int i=0;i<nums.length;i++){
            if(nums[i]!=val){
                nums[let]=nums[i];
                let++;
            }
        }
       return let;
    }
}

简单题拿下拿下！虽然脑子很乱不过也是独立思考完成了哈哈 李阳，我知道你不会复习！

26. 删除有序数组中的重复项

李阳你就是大傻逼，没有思想的东西，只会抄答案，最简单的也不会做…给你一个 非严格递增排列 的数组 nums ，请你 原地]删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k。去重后，返回唯一元素的数量 k。

nums 的前 k 个元素应包含 排序后 的唯一数字。下标 k - 1 之后的剩余元素可以忽略。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4,_,_,_,_,_]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

题解

class Solution {
    public int removeDuplicates(int[] nums) {
        int let =0;
        for(int i=1;i<nums.length;i++){
           if(nums[i]!=nums[let]){
             let++;
             nums[let]=nums[i];
           }
        }
        return let+1;
    }
}

啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊 日了狗了，这么简单没想到 当快指针元素不等于慢指针元素时，将值复制给慢指针，并且++，返回长度+1的数值

169. 多数元素

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入：nums = [3,2,3]
输出：3

示例 2：

输入：nums = [2,2,1,1,1,2,2]
输出：2

题解：

class Solution {
    public int majorityElement(int[] nums) {
        int count = 1;
        int maj = nums[0];
        for (int i = 1; i < nums.length; i++) {
            if (maj == nums[i]) {
                count++;
            } else {
                count--;
                if (count == 0) {
                    // 当计数归0时，将当前元素设为新候选者，重置计数为1
                    maj = nums[i];
                    count = 1;
                }
            }
        }
        return maj;
    }
}

1. 通过一个计数器count初始化出现数量为1，初始化maj为数组首元素。
2. 遍历数组：若当前元素与 maj 相同，count++；不同就count--；
3. 当 count == 0 时，将当前元素设为新的 maj，并重置 count = 1（因为当前元素是新候选者，至少出现一次）。
4. 最终 maj 就是多数元素。

示例验证（以 nums = [2,2,1,1,1,2,2] 为例）
初始：maj=2，count=1。
i=1（元素 2）：相同，count=2。
i=2（元素 1）：不同，count=1。
i=3（元素 1）：不同，count=0 → 重置 maj=1，count=1。
i=4（元素 1）：相同，count=2。
i=5（元素 2）：不同，count=1。
i=6（元素 2）：不同，count=0 → 重置 maj=2，count=1。
最终返回 2（正确，2 是多数元素）。

世界上怎么会有如此精妙的算法

189. 轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

题解

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[(i + k) % n] = nums[i];
        }
        System.arraycopy(arr, 0, nums, 0, n); 
    }
}

太他妈妙了… ….

121.买股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

题解

class Solution {
    public int maxProfit(int[] prices) {
        int max=0;
        int min=prices[0];
        for(int i=1;i<prices.length;i++){
            if(prices[i]<min){
                min=prices[i];
            }else{
                if(max<prices[i]-min){
                    max=prices[i]-min;
                }
            }
        }
        return max;
    }
}

hhhhh复习写出来啦

122. 买股票的最佳时机2

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。然而，你可以在 同一天 多次买卖该股票，但要确保你持有的股票不超过一股。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0。

题解

贪心和暴力求解有啥区别

class Solution {
    public int maxProfit(int[] prices) {
        int count=0;
        for(int i=1;i<prices.length;i++){
            if(prices[i]>prices[i-1]){
                count+=prices[i]-prices[i-1];
            }
        }
        return count;
    }
}

55.跳跃游戏

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

啊啊啊啊啊啊啊啊啊啊啊啊啊啊好难。第一遍就超时了

题解

class Solution {
    public boolean canJump(int[] nums) {
        int min=nums.length-1;
        for(int i=nums.length-2;i>=0;i++){
            if(nums[i]+i>min){
                min=i;
            }
        }
        return min==0;
     }
 }
例 1：nums = [2,3,1,1,4]倒序遍历：
i=3：1+3=4 ≥ min=4 → min=3
i=2：1+2=3 ≥ min=3 → min=2
i=1：3+1=4 ≥ min=2 → min=1
i=0：2+0=2 ≥ min=1 → min=0
最终 min=0 → 返回 true（正确）。

45.跳跃游戏2

给定一个长度为 n 的 0 索引整数数组 nums。初始位置在下标 0。

每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说，如果你在索引 i 处，你可以跳转到任意 (i + j) 处：

• 0 <= j <= nums[i] 且
• i + j < n

返回到达 n - 1 的最小跳跃次数。测试用例保证可以到达 n - 1。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

题解

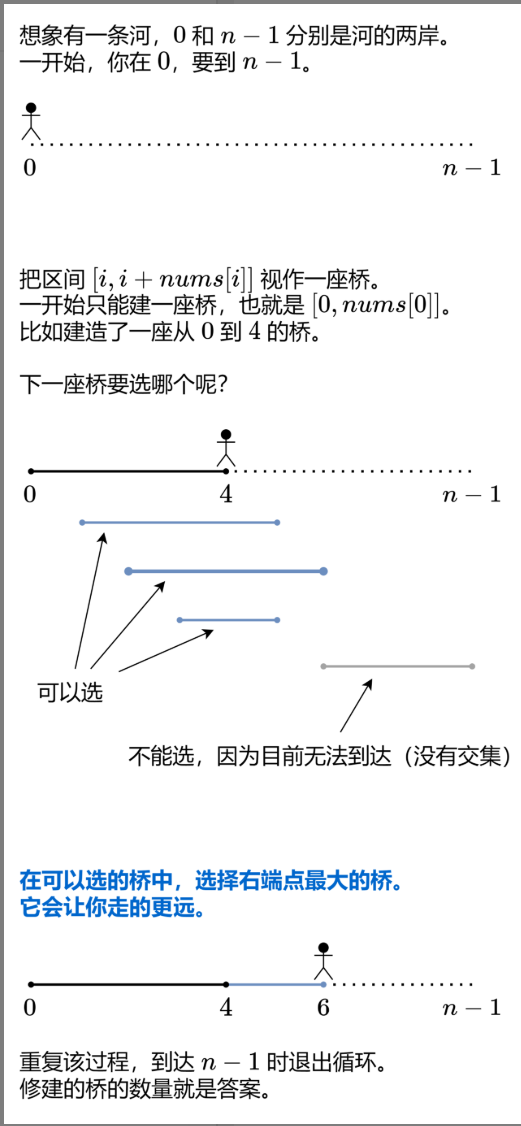
• 你站在数组的第 0 个位置（起点），要跳到最后一个位置（终点，下标是 n-1）。
• 数组里每个元素 nums [i] 是 “权限”：比如 nums [0] = 2，说明你在位置 0 时，最多能往后跳 2 步（可以跳 1 步到位置 1，也能直接跳 2 步到位置 2）。
• 跳的时候不能超出数组范围，而且题目保证一定能跳到终点，不用考虑跳不到的情况。

class Solution {
    public int jump(int[] nums) {
        int ans=0;
        int curRight = 0; // 已建造的桥的右端点
        int nextRight = 0; // 下一座桥的右端点的最大值
        for(int i=0;i<nums.length-1;i++){
            nextRight=Math.max(nextRight,i+nums[i]);
            if(i==curRight){
                curRight=nextRight;
                ans++;
            }
        }
        return ans;
    }
}

头昏昏的啥都看不懂

我是大傻逼

247. H指数

翻译：数组中有h个不小于h的值，求最大的h

给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。

根据维基百科上 h 指数的定义：h 代表“高引用次数” ，一名科研人员的 h 指数 是指他（她）至少发表了 h 篇论文，并且 至少 有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值，h 指数 是其中最大的那个。

示例 1：

输入：citations = [3,0,6,1,5]
输出：3 
解释：给定数组表示研究者总共有 5 篇论文，每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
     由于研究者有 3 篇论文每篇 至少 被引用了 3 次，其余两篇论文每篇被引用 不多于 3 次，所以她的 h 指数是 3。

示例 2：

输入：citations = [1,3,1]
输出：1

题解

class Solution {
    public int hIndex(int[] citations) {
        // [3,0,6,1,5] -> [0,1,3,5,6]
        Arrays.sort(citations);
        int h = 0, i = citations.length - 1; 
        while (i >= 0 && citations[i] > h) {
            h++; 
            i--;
        }
        return h;
    }
}